Antes de comprender la relación que existe entre los bioprocesos y el modelamiento matemático, conozcamos un poco más de los bioprocesos y biorreactores (BR’s). Los BR’s son definidos como sistemas o dispositivos que proveen un ambiente biológicamente activo bajo condiciones controladas. Aunque estos sistemas pueden emplearse para fines de producción de compuestos meramente químicos, en bioprocesos se prefiere el empleo de microorganismos o parte de ellos para la generación de compuestos de valor agregado. Algunos tipos de microorganismos cultivados en BR’s incluyen a las bacterias, levaduras, hongos, células vegetales y animales.

Actualmente, existe una gran diversidad de tipos de BR’s, los cuales son empleados para diferentes fines biotecnológicos, como la producción de biomoléculas, cultivos microbianos, biorremediación, generación de bioenergía, entre otros. Estos sistemas son empleados tanto a escalas de laboratorio, como los matraces agitados, hasta los BR’s de acero inoxidable de escala industrial con volúmenes de operación en el orden de metros cúbicos. Cabe resaltar, que los biorreactores de escalas pequeñas suelen emplearse para fines de investigación, y los reactores de escalas mayores son comúnmente usados para fines de producción.

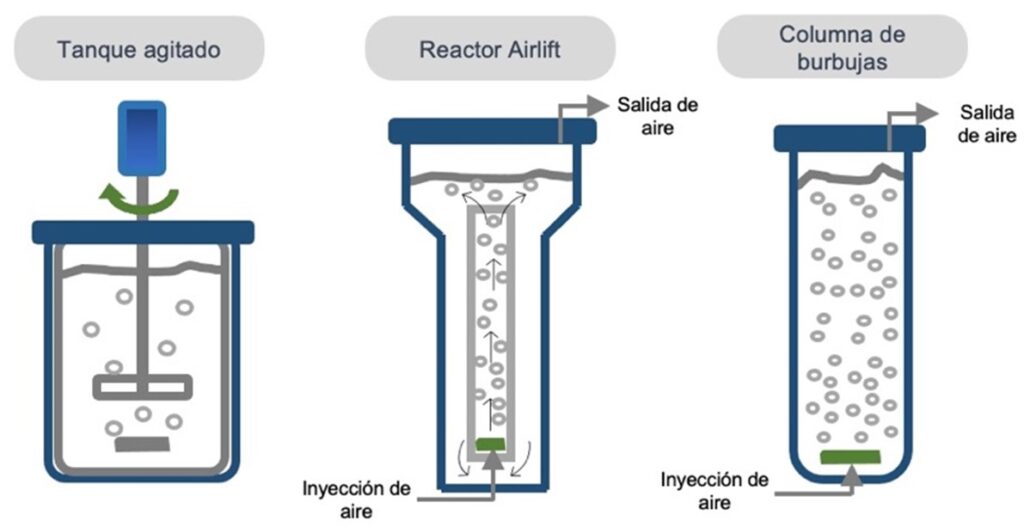
Algunos tipos de BR’s empleados en biotecnología se muestran en la Figura 1, los cuales pueden emplear agitación mecánica como el tanque agitado que emplea un motor para mantener mezclado el líquido en el contenedor; o neumática como el airlift y la columna de burbujas que usan inyección de aire para mantener condiciones homogéneas en el seno líquido.

Asimismo, los BR’s tienen diferentes modos de operación. Cuando un BR opera en modo por lotes (o batch), significa que el usuario coloca todos los reactivos en el dispositivo al inicio del cultivo y el sistema permanece cerrado hasta el final del experimento. Por otro lado, cuando existe un ingreso de material en el contenedor, pero no hay salidas, se dice que el BR opera en modo semicontinuo (o fed-batch). Finalmente, cuando un BR tiene entradas y salidas con los mismos flujos, se considera que el sistema opera en modo continuo. La elección del modo de operación del BR dependerá del objetivo que se persiga en el bioproceso, ya que cada modo puede presentar ventajas y desventajas, las cuales deberán evaluarse a detalle. Es importante señalar, que los BR’s permiten monitorear, manipular y controlar variables clave en el bioproceso, como la temperatura, el pH o la concentración de oxígeno en el medio. Cuando un bioproceso está en la etapa de investigación en laboratorio, generalmente se analiza el efecto de este tipo de variables en la producción del compuesto de interés, junto con otras de importancia relevante como la fuente de carbono y energía para el microorganismo, los flujos de entrada y salida, la agitación y la presión.

Ahora bien, como te podrás dar cuenta, el análisis de las variables antes mencionadas representa mucho trabajo experimental y de análisis, tomando en cuenta que cada variable afecta el ambiente del microorganismo generando diversas respuestas de este. Si esto es complicado, imagina analizar el efecto de estas variables sobre los cambios en el metabolismo del microbio. Basta recordar aquella red inmensa de las rutas metabólicas de un organismo para caer en la cuenta de que es un sistema realmente complejo de estudiar. Es aquí donde el modelado matemático entra en juego en el análisis de los procesos.

El modelado matemático puede entenderse como el proceso de traducción de un escenario del mundo real a un lenguaje matemático. Una vez creado el modelo matemático (generalmente un conjunto de ecuaciones), éste puede ser usado para realizar predicciones del comportamiento del sistema bajo escenarios diferentes. Cuando el modelo se somete a un análisis de validación experimental y estadística, solo entonces tendremos un modelo robusto capaz de predecir adecuadamente o analizar el sistema en un sentido más amplio. El análisis de un bioproceso con un simulador (modelo matemático) puede llevar a la disminución de costos de investigación, ya que al analizar escenarios diferentes podemos realizar experimentos muy puntuales para verificar los resultados predichos. La Figura 2 ejemplifica el proceso general del desarrollo de un modelo matemático y su empleo en el análisis de un proceso.

Cabe resaltar que existen diversos enfoques para la construcción de los modelos. Existen modelos estructurados y no estructurados. Los primeros consideran a la célula como un sistema complejo, empleando por tanto un conjunto múltiple de compuestos químicos para describir el bioproceso. Por ejemplo, estos modelos consideran diferentes nutrientes para el crecimiento microbiano, así como la generación de metabolitos que pueden promover o inhibir el crecimiento celular. Por su parte, los modelos no estructurados simplifican el comportamiento del metabolismo celular a una expresión matemática que describe la generación de células relacionada a un sustrato que limita su crecimiento (sustrato limitante). Algunos ejemplos de modelos no estructurados ampliamente utilizados para el análisis de bioprocesos son los modelos de Monod y Contois (Figura 2). Por otro lado, tenemos los modelos estocásticos y deterministas, el enfoque estocástico considera que la salida de un modelo (predicción) presenta una distribución de probabilidad (proceso aleatorio), dando a entender que, una vez resuelto el modelo la predicción no será la misma siempre. Por el contrario, el enfoque determinista enfatiza que el modelo producirá un solo conjunto de predicciones, es decir que a cada entrada le pertenece una sola salida.

Una vez propuesta la estructura del modelo cinético, es necesario validarlo experimentalmente. Este proceso cuantifica la concordancia o correspondencia entre la predicción del modelo y los datos experimentales para garantizar que el modelo es capaz de predecir escenarios reales. Este análisis se lleva a cabo mediante un software que implementa algún algoritmo capaz de reducir la diferencia entre el dato simulado y el dato experimental hasta un valor óptimo (Figura 2). El algoritmo Levenberg-Marquardt es un método de mínimos cuadrados amortiguados, el cual es considerado como uno de los más robustos para la solución de problemas de optimización.

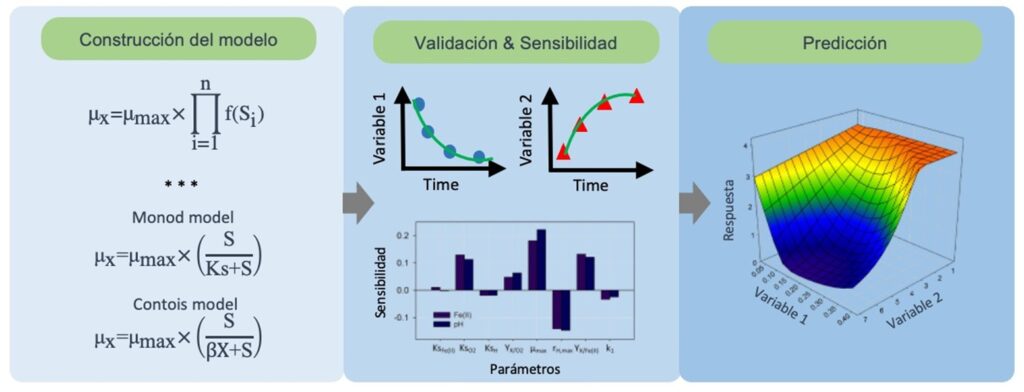
Dentro del conjunto de ecuaciones que conforman el modelo matemático, existe un conjunto de parámetros cinéticos que son estimados a partir de datos experimentales. Por ejemplo, en el modelo de Monod los parámetros cinéticos son la tasa específica de crecimiento (µ_max) y la constante de saturación (Ks). En el modelo de Contois, los parámetros son µ_max y ß. Una vez determinados los valores de los parámetros mediante algún algoritmo de optimización, estos suelen quedarse fijos al momento de realizar simulaciones. La importancia de su estimación radica en que algunos parámetros son muy sensibles, es decir que una pequeña variación puede llevar a cambiar drásticamente la predicción. Este estudio se lleva a cabo mediante un análisis de sensibilidad, el cual nos ayuda a saber en qué parámetros debemos fijar nuestra atención a la hora de estimarlos, y cuáles podemos descartar (los menos sensibles), de tal manera que nos lleve a reducir la complejidad del modelo sin perder robustez en la predicción.

Es importante mencionar que estas estas estructuras matemáticas son de gran ayuda a la hora de analizar los bioprocesos, ya que por medio de ellas podemos realizar análisis amplios del proceso, como el conocido análisis de bifurcación, el cual emplea un modelo matemático que simula un proceso operando en modo continuo para evaluar cómo afecta el flujo de entrada en el comportamiento de las variables del proceso. Este análisis permite observar también si existe multiplicidad de estados estacionarios en el sistema, es decir puntos de operación del BR donde no importante que tanto cambie el flujo de entrada o concentración de sustratos en la alimentación, las variables llegan al mismo punto de estado estacionario. Asimismo, el modelo puede usarse para analizar la estabilidad del sistema. Mediante el empleo de la conocida matriz jacobiana del sistema de ecuaciones, es posible determinar si la operación del biorreactor será estable en el punto de operación que nosotros como usuarios queremos. Una vez que sepamos que la operación del BR es estable podemos utilizar otro tipo de ecuaciones para regular nuestro proceso y llevarlo a cualquier punto de operación deseado. Este último tipo de ecuaciones son conocidas como leyes de control o controladores.

Como podrás ver, el desarrollo de modelos matemáticos validados con experimentos es de gran importancia para analizar bioprocesos. Aunque en esta columna nos enfocamos en el corazón del bioproceso (es decir el BR), la aplicación de las técnicas de modelado y simulación pueden ser empleadas para analizar procesos completos, es decir etapas de obtención de los sustratos e inóculo a emplear en el BR (upstream), así como las etapas de recuperación y purificación (downstream). La investigación en este campo incluye el desarrollo de modelos cinéticos complejos para analizar los bioprocesos de manera más puntual, el análisis de diversos tipos de bioprocesos mediante software con el fin de intensificarlos, el desarrollo de métodos y algoritmos que permitan calcular los valores óptimos de los parámetros cinéticos, así como la construcción de leyes de control cada vez más robustas.

Fotografía: Créditos de RickLawless via Wikimedia Commons